Multiplying and Dividing Fractions
This week we will be looking at some helpful approaches for solving multiplication and division problems of fractions.
Common Denominator Approach
There are several different methods we can use to help divide fractions. One of the approaches I find helpful for students, is the Common Denominator Approach. Lets take a look at an example!
Here we can see that the denominators are DIFFERENT. In order to divide them, we must give them both a COMMON denominator. Here, the best denominator (least common denominator) would be 6.
So, you would multiply BOTH of your denominators by a number that would give you 6. Then you would multiply that same number to both your numerators.
Here, we would multiply our denominator by 3, to get 6. Next, do the same to our numerator, which gives us 3/6.
Now that we have COMMON denominators, we can divide the problem. We know that 6 divided by 6 is just 1, so we can simply divide our numerators. 4 divided by 3 gives you 1 with a remainder of 1, which we put over 3, giving us a final answer of 1 and 1/3.
Just to make there is no confusion, lets try another example!
Once again, we must take our denominators that are DIFFERENT and make them COMMON. So, the least common denominator for this problem is 40.
Remember, we are taking our denominator, and multiplying it by a number that gives us 40. Then, take that number (5) and multiply it by the numerator as well.
Here, we multiply 10 by 4 to get 40. Then, we do the same for the numerator (2 x 4 =8)
Ok! Now we have COMMON DENOMINATORS again! Lets divide!
15 divided by 8 gives you 1, with a remainder of 7. To write this as a fraction, we would place the remainder on top of 8 (7/8). Our final answer is 1 and 7/8.
Multiplying Fractions Using the Area Model
When we are trying to multiply 2 fractions with different denominators, it sometimes helps to use a visual method to help understand what is really happening in the operation of multiplication. The area model helps students visualize the process of multiplication and understand how fractions look when drawn out. Below is an example of using the area model to multiply two fractions.
The problem reads : 2/5 x 3/4 =
When we use the area model approach, it helps to draw one of the fractions horizontally and the other vertically. 2/5 is drawn as 5 horizontal rows, with 2 of them shaded in (to represent two fifths). 3/4 is drawn as 4 vertical rows, with 3 shaded in (to represent three fourths).
 Next, we must combine both units together, to make one big unit that represents a new fraction. If we take 2/5 we get 5 rows across. When we take 3/4s, we add 4 rows going down. This gives us a new unit, with 20 squares. 2/5(yellow) and 3/4(pink) overlap and we now get a new fraction. 6/20 (the 6 orange squares) were made when we combined 2/5(yellow) and 3/4 (pink) together.
Next, we must combine both units together, to make one big unit that represents a new fraction. If we take 2/5 we get 5 rows across. When we take 3/4s, we add 4 rows going down. This gives us a new unit, with 20 squares. 2/5(yellow) and 3/4(pink) overlap and we now get a new fraction. 6/20 (the 6 orange squares) were made when we combined 2/5(yellow) and 3/4 (pink) together.
To check your answer, simply multiply your numerators, and your denominators!
Need more practice? Check out the links provided below!! There are some great videos which help explain all operations with fractions and include this method as well!
I have also included some worksheets for extra practice!!

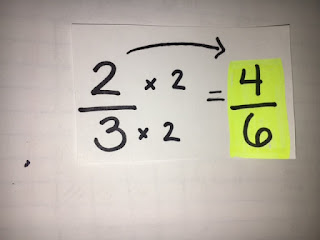







No comments:
Post a Comment